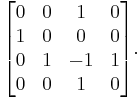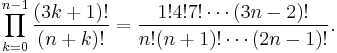Alternating sign matrix
In mathematics, an alternating sign matrix is a square matrix of 0s, 1s, and −1s such that the sum of each row and column is 1 and the nonzero entries in each row and column alternate in sign. These matrices arise naturally when using Dodgson condensation to compute a determinant. They are also closely related to the six vertex model with domain wall boundary conditions from statistical mechanics. They were first defined by William Mills, David Robbins, and Howard Rumsey in the former context.
For example, the permutation matrices are alternating sign matrices, as is
The alternating sign matrix conjecture states that the number of  alternating sign matrices is
alternating sign matrices is
This conjecture was first proved by Doron Zeilberger in 1992. In 1995, Greg Kuperberg gave a short proof based on the Yang-Baxter equation for the six vertex model with domain wall boundary conditions, that uses a determinant due to Anatoli Izergin, which solves recurrence relations due to Vladimir Korepin.
Razumov–Stroganov conjecture
In 2001 A.Razumov and Y.Stroganov conjectured a connection between O(1) loop model, fully packaged loop model (FPL) and ASMs. This conjecture was proved in 2010 by Cantini and Sportiello.
References and further reading
- Bressoud, David M., Proofs and Confirmations, MAA Spectrum, Mathematical Associations of America, Washington, D.C., 1999.
- Bressoud, David M. and Propp, James, How the alternating sign matrix conjecture was solved, Notices of the American Mathematical Society, 46 (1999), 637-646.
- Kuperberg, Greg, Another proof of the alternating sign matrix conjecture, International Mathematics Research Notes (1996), 139-150.
- Mills, William H., Robbins, David P., and Rumsey, Howard, Jr., Proof of the Macdonald conjecture, Inventiones Mathematicae, 66 (1982), 73-87.
- Mills, William H., Robbins, David P., and Rumsey, Howard, Jr., Alternating sign matrices and descending plane partitions, Journal of Combinatorial Theory, Series A, 34 (1983), 340-359.
- Razumov, A.V., Stroganov Yu.G., Spin chains and combinatorics, Journal of Physics A, 34 (2001), 3185-3190.
- Razumov, A.V., Stroganov Yu.G., Combinatorial nature of ground state vector of O(1) loop model, Theor. Math. Phys., 138 (2004), 333-337.
- Razumov, A.V., Stroganov Yu.G., O(1) loop model with different boundary conditions and symmetry classes of alternating-sign matrices, Theor. Math. Phys., 142 (2005), 237-243.
- Robbins, David P., The story of
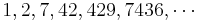 , The Mathematical Intelligencer, 13 (2), 12-19 (1991).
, The Mathematical Intelligencer, 13 (2), 12-19 (1991). - Zeilberger, Doron, Proof of the alternating sign matrix conjecture, Electronic Journal of Combinatorics 3 (1996), R13.
- Zeilberger, Doron, Proof of the refined alternating sign matrix conjecture, New York Journal of Mathematics 2 (1996), 59-68.
External links
- Alternating sign matrix entry in MathWorld